First steps on strategy (part 1/3?)

Hi folks,

I have been pleased to see the initial interest in Aces’ Nim. At first glance the game may seem like an exercise in brute-forcing through the game tree – an approach that might be possible (if tedious) for small boards, but quickly becomes infeasible on large boards. I have tried to craft the boards in the Designed Boards section to suggest ideas for how one might evaluate a board without resorting to brute force, but I figured it was also worth writing a brief post about the ideas I was hoping to convey at least for the first steps of that journey.

This post is a bit of an experiment, as I am not sure whether anyone will really read it, especially in this devlog space. If it seems to be successful then I may follow up with another post on some more advanced strategy ideas. I’m also going to be splitting it up into 2 or 3 parts for readability, as it is turning out to be fairly long.

Arguably this post is a spoiler! If you would prefer to figure everything out yourself from first principles, then you should probably stop reading here.

All the ideas in this post can also essentially be found in Winning Ways For Your Mathematical Plays by Berlekamp, Conway, and Guy. These ideas were also presented by Berlekamp in his Youtube series discussing impartial combinatorial games.

We’ll start by thinking about the Optional Burn ruleset, since that’s where the designed boards start (and since it is ultimately much simpler to analyze than the Mandatory Burn ruleset – that small rule change has surprisingly large consequences). And, to keep things simple, we’ll start by analyzing the case where there’s just one rank of cards on the board, say Jacks.

The first thing you’re likely to notice in the first few boards is that you can break down the board into several non-interacting strips of consecutive cards, separated by blank spaces. And in the single-rank case, all we really care about is how many cards are in each of those strips.

You’re also likely to quickly notice that – especially on single-rank boards – the scores that actually appear have a very limited range of values. In particular, you will always move first and collect a Jack for 1 point, yielding a score of +1; then the computer will reply and collect a Jack for 2 points, moving the score back to −1; your reply, earning two points, moves the score back to +1; and the score will continue ping-ponging between +1 and −1 until eventually all cards are collected. If you took the last move the final score will be +1; if the computer did, the final score is −1. So in the single-rank case, the game boils down to ensuring that you make the last move.

This allows an early and critical strategic observation: if you can hand the computer a board consisting of two strips of the same length, say one on the left side of the board and one on the right, then you can easily force a victory. Whatever move the computer makes, say to collect a card in the left strip, you can easily mirror in right strip, collecting a card in the same spot. If the computer then makes a move in what remains of the right strip, then you can mirror that move back over to the left, and so on. By keeping the left and right side of the board identical at the end of each of your moves, you can guarantee that you will always have a reply to the computer’s move, since its move on one side of the board cannot make its mirror-image on the other side invalid. So when the board is finally empty it must be the computer, and not you, that ends up facing an empty board – meaning you will finish with a positive score.

From this observation one can immediately deduce that any single-rank board with just a single strip is a board you can win going first: just take either one or two cards from the middle of the strip so that the resulting two strips have the same length, and then apply the mirroring strategy given above. A similar idea can be applied to the board below: after taking the card outlined in cyan, we see that any move by the opponent in one of the length-3 strips can be mirrored in the other strip, and similarly for the length-1 strips:

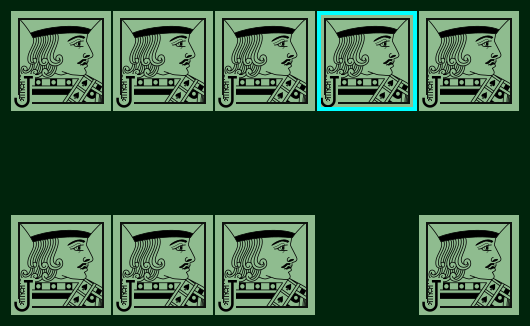
This idea may appear to be trivial and limited at first, but we will soon see that it is more powerful than it first appears, if we suitably expand our idea of what it means for two strips to be "the same". In fact, this idea in some sense underlies all of the strategy in Aces’ Nim.

To proceed further it will be helpful to introduce some notation. Let’s write T₁ for a strip consisting of just a single card, T₂ for a strip of two cards, and so on. (Here the T stands for opTional; using the letter O would be too confusing because it looks like a zero, and using P would be too confusing for reasons that will soon become clear.) We’ll use the familiar + sign to indicate that we’re putting two strips next to each other separated by blank space, so that – for example – the board written above could be written as T₅ + T₃ + T₁. Going forward, I will likely be using the words "board" and "position" interchangeably, with "position" being the more standard term used in the wider literature.

Now, looking at any position, the same moves are available whether it’s your turn or whether it’s the computer’s turn. So either the Next player to move has a win in that position, or the Previous player has a strategy to ensure a win regardless of what move is made. The usual convention here is to say that a position is an 𝒩-position if the Next player can force a win, and a 𝒫-position is the Previous player can force a win even against perfect play. So, for example, our mirroring argument shows that T₅ is an 𝒩-position: the next player can take the middle card, moving to T₂ + T₂, and thereafter play the mirroring strategy to force a win. By the same token T₂ + T₂ is itself a 𝒫-position: the player who is handed T₂ + T₂ is now the "next" player, but we know that any move they make can simply be mirrored back.

The simplest board of all is the board with no cards. We will write 0 to stand for that board. We would never really want to think about a board with no cards as a starting position, but it is important to consider as a position that the game can end at. In that context we should consider 0 to be a 𝒫-position: the player who eventually finds themselves as the "next" player facing an empty board has lost the game, so their opponent, who just played previously, was the winner.

Our usage of the symbol 0 together with the plus sign suggests that there also should be some notion of "equality" here where, for example T₅ + 0 = T₅: after all, T₅ + 0 literally just means "a strip of 5 cards, followed by a blank space and then nothing", which should mean the same thing as just "a strip of 5 cards". There are a few different ways in the literature to define equality between these kinds of game positions, but we will use the following: for positions X and Y we will say that X = Y if X + Y is a 𝒫-position.

This definition may seem strange, but it agrees with many of the properties we would expect = to have: for example, X = X for any position X, because the statement that X = X just means that X + X is a 𝒫-position, and that’s exactly what the mirroring argument shows. Also, X + 0 = X for any position X, because the statement that X + 0 = X just means that (X + 0) + X is a 𝒫-position, which again follows just by the mirroring argument.

This post is getting a bit long, so this seems like a good place to leave off. In the next part of the post, we will continue discussing equality of game positions. Until then I will leave off with the following question you may find fruitful to consider: is T₁ = T₄?

Continue to part 2